OptiFloat.jl

This package is a work in progress

This package contains only a proof of concept and has not yet been tested on more complex examples.

What is OptiFloat?

OptiFloat.jl rewrites floating point expressions to more accurate alternatives. It is a pure Julia implementation of Herbie. For example, the function f

f(x) = sqrt(x+1) - sqrt(x)

is inaccurate for x>1, because it subtracts two floating point values that are close to each other. Calling f with e.g. a Float16 we get an inaccurate result:

julia> f(Float16(3730))
Float16(0.03125)

Compare to the more accurate Float64 result:

julia> f(3730.0)
0.00818627789193016

OptiFloat.jl rewrites this expression to a more accurate equivalent (using the original, low precision Float16!):

julia> using OptiFloat

julia> g = @optifloat sqrt(x+1)-sqrt(x) T=Float16 batchsize=100
#1 (generic function with 1 method)

julia> g(Float16(3730))
Float16(0.00819)

If we plot g we can see that it matches the more costly, higher precision evaluation of f:

using CairoMakie

fig = Figure()
a1 = Axis(fig[1, 1]; xscale=log10, xlabel="x", ylabel="f(x)")
xs = Float16.(logrange(1, 4000, length=100))
lines!(
    a1, xs, f.(xs);
    color=1, colorrange=(1, 10), colormap=:tab10, linewidth=3,
    label="f(x) = sqrt(x+1) - sqrt(x) (Float16)"
)
lines!(
    a1, xs, f.(Float64.(xs));
    color=2, colorrange=(1, 10), colormap=:tab10, linewidth=3,
    label="f(x) = sqrt(x+1) - sqrt(x) (Float64)"
)
lines!(
    a1, xs, g.(xs);
    color=3, colorrange=(1, 10), colormap=:tab10, linestyle=:dash,
    label="g(x) = 1/(sqrt(x+1) + sqrt(x)) (Float16)", linewidth=3
)
axislegend(a1)
fig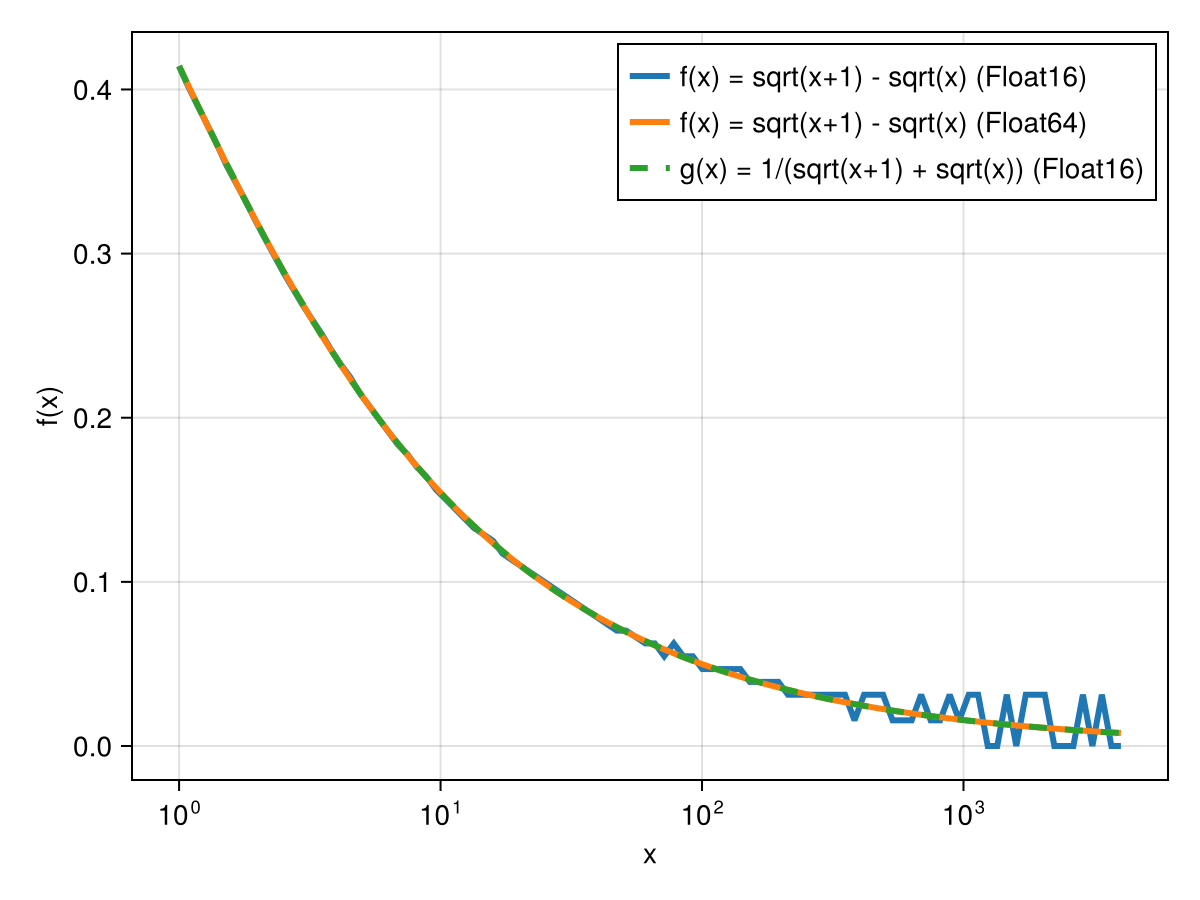

INFO

For more details on how OptiFloat.jl works and how to customize it to your needs, check out OptiFloat under the hood.

Acknowledgements

OptiFloat.jl is built on top of a number of great Julia packages. Most notably:

• Metatheory.jl for everything related to expression rewriting & simplification.

• DynamicExpressions.jl for computing local errors of floating point expressions.

• IntervalArithmetic.jl to evaluate expressions on Interval{BigFloat} with arbitrary precision.